以下のプログラムは,ユーザから入力された100個の点の座標について,それらの点の中からいずれか3つを選択して作ることのできる三角形のうち,最大の面積を有するものについて,その三角形を構成する頂点の番号および面積を出力するものである.
(1) 空欄では何を行うべきか考え,行うべき処理を C言語で記せ.なお,新たに変数を使う場合は変数の宣言を追加せよ.
|
#include <stdio.h> |
(2) このプログラムの効率性を評価したい.関数 SquareMeasure() が呼び出される回数ができるだけ少ない方が効率がよいものと考える.自分の考えたやり方では,呼出回数は何回になるかを理由をつけて示せ.
プログラムでは,点の2次元座標を格納するために2次元配列を用いている.2次元配列自体の説明については Google先生 がよく教えてくれる.例えば このページ などがわかりやすい.
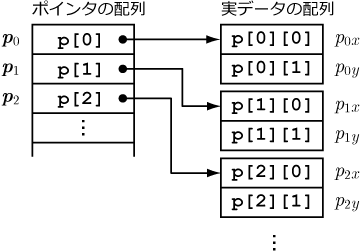
このプログラムでは (NUM)×(2) の要素数の2次元配列を用いている.i 番目の点の x, y 座標はそれぞれ,p[i][0],p[i][1] に格納される.
重要なことは,この2次元配列において p[i] と書いた時,これは i 番目の点の x 座標・y 座標を格納した要素数2の1次元配列の先頭アドレスを示すポインタを意味している ということである.このプログラムでは関数 SquareMeasure() を使って3角形の面積を求めるが,この際関数に引数として渡してやる情報は,求める3角形の3つの頂点の座標を格納した3つの1次元配列それぞれの先頭アドレスである.関数の3つの引数がみな double * 型をしているのは,double 型の1次元配列の先頭アドレス (ポインタ) であるという意味である.例えば 1番,3番,7番の3つの点を頂点とする3角形の面積は SquareMeasure(p[1], p[3], p[7]) として求める.

Fig.1 2次元配列
前回とほとんど同様の問題であり,今回は「全ての2点の組み合わせ」でなく「全ての3点の組み合わせ」を網羅しなくてはならない点が異なる.3点を網羅する場合,三重ループを使い,1点目 i のループは 0 番から NUM-3 番まで,2点目 j は i+1 から NUM-2 番まで,3点目 k は j+1 から NUM-1 番 (最後) まで 回せばよい.
なぜそれでよいかについて考えてみよう.例えば点の数が5個である場合,点の番号は0番から4番までとなる.ここから3点を取り出す組み合わせを網羅するとき,「順列」ではなく「組み合わせ」であるという意味は,例えば1番,3番,4番という3点を考えるとき,その点番号の順列は 1-3-4,1-4-3,3-1-4,3-4-1,4-1-3,4-3-1 の 6通りあるが,これらについてそれぞれ合計6回面積を計算することが無意味であることは自明 (全部が同じ三角形を表している) であり,これらの組み合わせから1通りだけを取り出して面積を計算すればよいことは明らかである.それを行う方法は,「小さい順の場合だけを取り出す」などを行えばよいのである.5点の場合,小さい順に取り出していく方法は以下のようになる.
0-1-2
0-1-3
0-1-4
0-2-3
0-2-4
0-3-4
1-2-3
1-2-4
1-3-4
2-3-4
ここで点を取りだしていく順番のルールは最初に示した通りであり,正しく 5C3 = 5⋅4⋅3/(3⋅2⋅1) = 10 通り行っていることが分かる.
繰り返し回数については,前回の課題と同様であり,NUM点から3点を選ぶ組み合わせの数 NUMC3 回となる.
面積については,授業中に説明したとおり,三角形を構成する2つの3次元ベクトル (z 成分は0) の外積 (x, y 成分は0) の z 成分の絶対値の半分が三角形の面積である.
外積 (outer product) とは,2つのベクトルのかけ算の一つであり (もう一つは内積 (innner product)),演算の結果はベクトルとなる.演算子は "×" と表記する.外積の計算方法については,
であるとき,
と計算する (一般的に,斜体・太字で書かれた小文字の変数はベクトルを表す).
Fig.2 には,c = a×b を示した.外積ベクトルの方向は,もとの2つのベクトルに直交し,一つめのベクトルから二つめのベクトルへ向かってネジを回したときにネジが進む向きである.つまり,図の場合 c = b×a であればベクトル c の向きは下向きとなる.外積ベクトルの大きさ (長さ) は |c| = |a||b|sinq であり,これはベクトル a と b が構成する平行四辺形 (図中黄色部分+オレンジ色部分) の面積に等しい(底辺 |a| に 高さ |b|sinq をかけている).
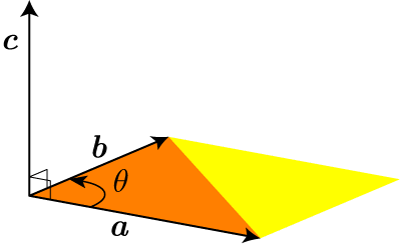
Fig.2 三角形の面積と外積
これを使って平面上の三角形の面積を計算する方法は以下の通りである.まず,三角形を構成する点の座標 (位置ベクトル) を p0,p1,p2 とするとき,三角形を構成する 2つのベクトル a と b は,
a = p1−p0
b = p2−p0
と設定する.さらにこれらを空間上の3次元ベクトルとして,z 座標をそれぞれ 0 と設定する (xy-平面上のベクトル).
次に外積の演算を行うが,2つのベクトルの z 座標は両方 0であることから,外積ベクトルの x 座標,y 座標は 0となり,z 座標の値は ax by−ay bx となる.つまりまとめれば,z 座標の値は,
(p1x− p0x)⋅(p2y− p0y) − (p1y− p0y)⋅(p2x− p0x)
となる.三角形の面積を求める関数 SquareMeasure() においては,この値の絶対値の半分を求めて返せばよい.
忘れてはいけないことが2点ある.
第1点は,ベクトル a と b の位置関係次第では,外積ベクトルは z 軸の負の方向を向き,その z 座標は負となる可能性もあるという点である.この点に対処するために,得られた z 座標の値の絶対値を撮る必要がある.これに使われるのが fabs() という関数である.この関数を使うためにはヘッダファイル math.h をインクルードする必要がある.ただし,これを利用せずに "if (x < 0) x = -x;" (x は外積の値) などとしても同じであり,この場合 math.h をインクルードする必要はなくなる.実はこちらの方がすっきりしていて処理速度も若干速い.
第2点は,得られた絶対値の値は平行四辺形の面積 (図中黄色) を表しているということである.三角形の面積 (図中オレンジ) を求めるためには,これを 0.5倍しなくてはならない.
(1) ソースコード例を以下に示す.赤い文字で示した部分が書き加えるべき内容である.ただし,このコードでは,100個の点座標をユーザが手入力する代わりに乱数を用いて点座標を与えている.
|
001: #include <stdio.h> 002: #include <stdlib.h> // 乱数発生関数 drand48() のため 003: #include <math.h> // 絶対値関数 fabs() のため 004: 005: #define NUM 100 // 点の数を指定 006: 007: // 関数 SquareMeasure() のプロトタイプ宣言 008: double SquareMeasure(double *, double *, double *); 009: 010: int main(int argc, char *argv[]) 011: { 012: int i, j, k; // 汎用変数 013: double p[NUM][2]; // 点の座標の配列 (2次元配列) 014: double s; // 面積の一時保存先 015: double max; // 「今のところの最大面積」 016: int points[3]; // 見つかった三角形の点番号 017: 018: 019: srand48(0); // 乱数の種を初期化 020: 021: // NUM個の点座標を乱数により設定 022: for (i = 0; i < NUM; i++) { 023: p[i][0] = 10.0 * drand48() - 5.0; 024: p[i][1] = 10.0 * drand48() - 5.0; 025: } 026: 027: max = 0.0; // max の初期化(最初は小さい数) 028: 029: // メインの三重ループ 030: for (i = 0; i < NUM - 2; i++) 031: for (j = i + 1; j < NUM - 1; j++) 032: for (k = j + 1; k < NUM; k++) { 033: // sに面積を代入 034: s = SquareMeasure(p[i],p[j],p[k]); 035: 036: // maxより更に大きい面積の三角形が見つかった場合 037: if (s > max) { 038: max = s; // max を更新 039: points[0] = i; // 点番号の保存 040: points[1] = j; 041: points[2] = k; 042: } 043: } 044: 045: // 結果の表示 046: printf("Largest triangle: p[%d]-p[%d]-p[%d]", 047: points[0], points[1], points[2]); 048: printf("\nSquare Measure = %f\n", max); 049: 050: return 0; 051: } 052: 053: // 三頂点の座標から三角形の面積を求める関数-1 054: double SquareMeasure(double *p0, double *p1, double *p2) 055: { 056: double tmp; 057: 058: // 外積の z成分 → tmp 059: tmp = (p1[0]-p0[0]) * (p2[1]-p0[1]) - (p1[1]-p0[1]) * (p2[0]-p0[0]); 060: 061: // 負の時は -1倍 062: if (tmp < 0) tmp *= -1.0; 063: 064: // 半分を返す 065: return(tmp * 0.5); 066: } 067: 068: // 三頂点の座標から三角形の面積を求める関数-2 069: double SquareMeasure2(double *p0, double *p1, double *p2) 070: { 071: // 外積の z成分の絶対値の0.5倍を返す 072: return(0.5 * fabs((p1[0]-p0[0]) * (p2[1]-p0[1]) - 073: (p1[1]-p0[1]) * (p2[0]-p0[0]))); 074: } |
まず001〜003行ではヘッダファイルのインクルードをしている.浮動小数点数の絶対値を求める関数 fabs() を利用するためには math.h もインクルードする必要がある場合がある.ただし,stdlib.h は関数 drand48(), srand48() を利用するためにインクルードしており,通常は不要.
005行では点の数 NUM をプリプロセッサにより定義している.以後,プログラム上の NUM という文字列は 100 という文字列に読み替えられた上でコンパイルされることになる.
007行では面積を求める関数 SquareMeasure() のプロトタイプ宣言を行っている.プロトタイプ宣言について理解できていない場合は,例えば このページ を参照せよ.プロトタイプ宣言の利点は,関数の内容をその関数を呼び出す以前に書かなくてはならないという制約をなくすること,および関数の引数,返値をコンパイラがきちんとチェックしてくれることである.プログラムの冒頭でプロトタイプ宣言を行っておけば,関数の実体はプログラム中のどこに書いても良い.なお,プロトタイプ宣言では引数の名前は必ずしも書く必要がないが,参考ホームページにあるとおり,きちんと引数名まで書いておく方がよい.
010行から始まる main関数では,まず 012行から 016行で,main関数内で用いるローカル変数を宣言している.i, j, k は汎用変数であり,一般的に i, j, k, l, m, n あたりの変数名は,汎用変数として for文などで用いる.p[NUM][2] は,点の座標を格納するための2次元配列である.double型の max は,各段階においてそれまでに見つけた最大の面積を格納しておく変数であり,points[3] は,それまでに見つかった最大の三角形を構成する3頂点の頂点番号を保存しておくための配列である.
前回の課題において述べたのと同様に,関数 SquareMeasure() を無駄に呼び出すことを避けるために double 型の変数 s を用意し,各3頂点に対して求めた面積をまずこの変数に格納し,max との比較やその更新においてこの変数を用いることによって効率を高めることができる.
022〜025行では,NUM個の点の座標を入力している.問題として与えたのは scanf() による手入力のコードであるが,ここでは乱数を用いて範囲 [-5, 5) の一様乱数を座標値に代入している.この乱数を求めるのに用いているのは drand48() という関数で,この関数は引数なしで呼び出すと,返り値として範囲 [0, 1) の一様擬似乱数を返す.これを10倍して5を引くことで,求める範囲の一様乱数を得る.また,drand48() が出力する乱数系列を指定するための「乱数の種」を指定するため,019行で srand48() を種 0 として呼び出している.乱数については このページ その他のウェブ上のコンテンツや教科書の2-1節等を参照すること.
さて,ここからが心臓部である.「最大値を求める」作業においては,「今のところの最大値」である変数 max を用い,各時点で求めた面積が max より更に大きい場合に max をその面積で更新するという方法が用いられるが,これを行うためには,作業の最初に max を「考えられる限り一番小さい値以下の値」で初期化しておかねばならない.今回の場合,扱う問題が「三角形の面積」であるため,最小でも 0.0 であることが分かっているので,027行にあるとおり,max は 0.0 に初期化すればよい.
030行から032行にかけてが,「考え方」で示したとおり,3点をもれなく選択するための三重ループである.030行の最初のループでは,i を 0 から NUM-3 まで回す.このループの中で回る 031行の2番目のループでは,j を i+1 から NUM-2 まで回す.更にその中で回る 3番目のループでは,k を j+1 から NUM-1 (一番最後の点) まで回す.このように,1点目は最初から初めて最後から3番目の点まで回し,2点目は 1点目に選んだ点の次から,最後から2番目の点まで,3点目は 2点目に選んだ点の次の点から最後の点までを選ぶようにループを回すことによって,全ての点の組み合わせを小さい順 (昇順) で選択することができる.
このようにして,3点の組み合わせをもれなく選択するループができた.ループの内部では,i, j, k がそれぞれ,三角形の 1, 2, 3点目の頂点の番号に対応している.この三角形の面積を関数 SquareMeasure() により求め,一時保存用変数 s に代入しているのが 034行である.
次に,一時保存された面積の値を,ここまででの最大面積 max と比較し,更に大きい面積が求まっている場合 (037行の if文の条件式が真となったとき) は max をその面積の値に更新する (038行).更に,今回は面積だけでなく,その面積に対応する三角形の 3頂点の番号も求めなければならないので,i, j, k を配列 points[3] にそれぞれ保存する (039行から041 行).
以上の三重ループが全て周り,ループから抜けた時点で,全ての3点の組み合わせに対して求められた面積の最大値が max に,それに対応する 3頂点の番号がpoints[3]に格納されている.046〜48行では,これらの結果を表示している.
以上で main関数については終わりであり,次に面積を求める関数 SquareMeasure() を説明する.ここでは2通りの関数を示した.054〜066行に示したものでは,まず外積の z座標を変数 tmp に代入,次にこれが負の場合は -1倍し,最後にその値の半分を返している.069〜074行で示したものでは,浮動小数点数の絶対値を返す関数 fabs() を利用している.実は「関数を呼び出す」というだけでもコンピュータ上で一定の手間がかかることを考えると,前者のほうが処理速度が早い.
さらに改善点として,「0.5倍する」という操作を毎回行うのではなく,変数 max との大小比較の時点では倍の数字を比較し,最後の最後に画面に出力する直前で max *= 0.5; としてやる方が,半分にする計算の手間は省ける.
(2) 与えられた点から 3点を選択してできる三角形全てについて1度ずつ面積を計算すればよいので,面積を求める回数は,100点から 3点を求める組み合わせの数に等しく,
100C3 = 100⋅99⋅98 / (3⋅2⋅1) = 161700回.
一般に,点の数が n個である場合は,
nC3 = n(n-1)(n-2)/6回.
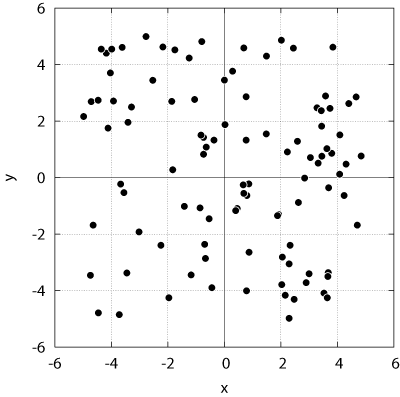
Fig.3 に,実行結果の例を示す.この例では,100個の点の座標を乱数によりランダムに与えている (はっきり言って,人の手で適当な100個の座標を入力するのは実はあまりにも大変).ここでは,x座標,y座標のそれぞれを,[-5.0, 5.0) の範囲の一様乱数として与えた.図中 (a) に,与えられた点群をプロットしたものであり,(b) は,選ばれた3点を結んでできた三角形を示している.得られた面積は 43.190587 であった.ちなみにこの設定での最大面積は 50.0 である.そのとき,二つの頂点は取り得る領域の正方形の隣り合う角にあり,最後の頂点は逆サイドの辺の上のどこかにある.
 |
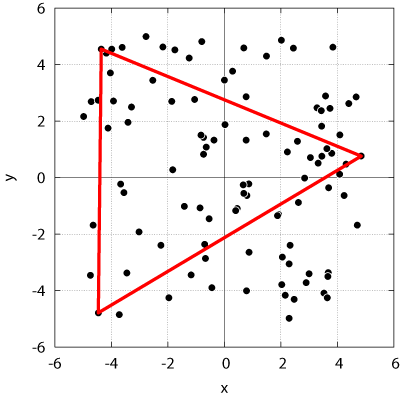 |
| (a) ランダムに生成した点群 | (b) 求められた最大の三角形 |
| Fig.3 実行結果の例 | |
発展的内容を含むソースコード例が このソースコード である.そのままコンパイルして実行することができる.ここでは発展的内容について簡単な概略を示すにとどめ,あとは学生各自の独学に任せたい.質問はいつでも受けてつけているので,授業の前後に聞きに来てくれてもよいし,自由な時間にE2棟801号室に聞きに来てくれても良い.
ただし!よいエンジニアを目指そうとするのであれば,「よく分かんないんでとりあえず聞く」という態度は避けるべきで,自分でいろいろと調べたり試したりする時間に上達への道があるのだということも意識し,それでもどうしても分からない場合に初めて聞くという方法を取ることを意識したほうが良い (これは卒業研究について,特にそう言える).
プログラムを作成するとき,自分の後継者が読む可能性がある場合や,そもそも一つのプログラムを多人数で分担して作成している場合など,他人がそれを読んでもすぐに理解できるようにするために,プログラムにはきちんとした注釈を入れなくてはならない.示した例ではプログラムの冒頭にプログラムの内容や使い方を表記したが,実際には関数一つ一つにもその関数がどういう内容のもので,どういう引数,どういう返値を持つかなどを詳細に記す.
これは面倒な作業に思えるかも知れないが,結局はこのように可読性を高めておくことが全体的な労力を低減することになる.なぜなら,プログラムを書く労力とは,一通りプログラムを書き上げる労力よりもむしろ,一度一通り書いたプログラムのバグをとること,一度きちんと動いたプログラムの仕様変更を行っていくことなどにあるからである.他人が書いた注釈なしのプログラムを改造するなどという作業は,一度やるともう二度とやりたくなくなる.そして更に重要なこと:自分自身が書いたプログラムですら,時間がたつと見たくもない有様になっていることが多い.
示したプログラム例では,main関数が引数・返値を持っている.これがどういうことかについては,引数については例えば このページ,返り値については例えば このページ などに分かりやすい解説がある.要するに,プログラムを呼び出す側 (多くはシェルであり,Windows でいうところのコマンドプロンプトになる) とプログラムとの間の情報のやりとりを司るのがこれらである.
示したプログラムをコンパイルした結果の実行ファイルが,例えば ex03.exe であったとするとき,このプログラムは4つまでの コマンドライン引数 をとることができる.以下に例を示す.
> ex03.exe 100 3 1 0
1つめの引数は点の数,2つめは乱数の種 (後述する),3つめは扱っているi, j, k を画面に表示するか否かを示すフラグ,4つめは生成された点群の頂点座標,選ばれた三角形の頂点座標をファイルに保存するか否かのフラグである.第1引数が省略された場合,プログラムはユーザに点の数の入力を促す.それ以外の引数が省略された場合には,デフォルトの値 (全て0) を用いる.
main関数が返す値は呼び出し側に伝えられる.通常は,プログラムが正常終了した場合には 0 を,異常終了した場合にはそれ以外の値を返すのが通常の流儀である.
示したプログラムでは,点の座標をユーザ入力ではなく乱数により与えている.乱数を発生するとき,C言語では,整数型の乱数を発生する関数 rand(),random() および浮動小数点数型の乱数を発生する関数 drand48() がよく使われる.ただし,これらの関数の発生する乱数は完全にランダムではなく,疑似乱数 と呼ばれる.
関数を呼ぶたびに発生される乱数の列の初期値として,乱数の種を与えると,これに応じた決まった数列が生成される.この「種」を与える関数は srand() や srand48() である.できるだけでたらめな値を得たい場合,乱数の種には現在時刻を与えるのが一般的であるが,決まった結果を得られるようにしたい (再現性が欲しい) 場合には,これを明示的に与える.
drand48() は double型の 0.0以上 1.0未満 (つまり [0, 1) の範囲) の一様乱数を与える関数である.プログラム例ではこれを 10.0倍して 5.0 を引くことで,[-5.0, 5.0) の範囲の一様乱数を得ている.
このプログラムでは,点の数をユーザが任意に決定できる.この結果,点の座標を格納しておくための配列のサイズをあらかじめ決定することができない.このような場合に使われるのが,メモリの動的確保 という方法である.解説ページは,例えばここ などがある.
動的確保を使うことによって,「想定しうる最大サイズの配列をあらかじめ確保しておく」などの無駄なメモリ消費を避けることができる.このプログラムでは,コマンドライン引数あるいはユーザ入力によって与えられた点の数を変数 num に格納し,これをサイズとする配列をメモリ動的確保関数 malloc() を用いて確保している.
このようにして動的に確保されたメモリ領域を開放するには free() を用いるが,プログラムの起動中に繰り返しメモリの確保・解放を繰り返すような場合でなければ,解放しなくても問題は起きない.なぜなら,メモリを解放せずにプログラムを終了すれば自動的に確保されたメモリ領域はシステムに返還されるからである.
メモリの動的確保については,この授業でそのうち扱う.
さらに,2次元配列を利用する場合,このメモリ確保の手順がもう一段必要となる点に注意が必要である.この場合の配列 p[NUM][2] について,配列 p[NUM] はdouble型ポインタの配列であり,一つ一つのポインタはそれぞれの点座標 (x座標・y座標) の2つのデータが入った要素数2の配列の先頭アドレスを示している.したがって動的確保には2段階が必要で,(1) ポインタ配列の動的確保,(2) ポインタ配列の各要素ポインタが参照しているそれぞれの double型配列の動的確保を両方やらなければならない.一つの方法は,(1) をすましたあとで,ポインタ配列の各要素に対して p[i] = (double *)malloc(sizeof(double) * 2); を繰り返し行う方法であるが,これだと座標値配列が連続してメモリ空間上に配置される保証がない.そこで,このコードでとっている方法は,(点の数)×2 のサイズの1次元配列を最初に確保し,その0番目,2番目,4番目,6番目…のアドレスを p[0],p[1],p[2],p[3],…に代入する方法である.詳しくは このページ を参照.また,コードの90行目で p[i] = p[0] + i * 2; としているのは,ポインタの演算ではバイト単位ではなく,そのデータ型のサイズ単位であるからであることにも注意せよ.